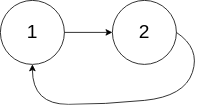
Linked List Cycle

Linked List, tortoise and the hare approach

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].

• -105 <= Node.val <= 105

• pos is -1 or a valid index in the linked-list.

Solutions

This is a method for detecting a cycle in a singly-linked list using the Floyd’s cycle-finding algorithm, also known as the tortoise and the hare algorithm.

Steps

1. Check for empty or single node list: If the list is empty or only contains a single node, it cannot contain a cycle, so return false.

2. Initialize two pointers slow and fast: The slow pointer moves one step at a time, while the fast pointer moves two steps at a time.

3. Detect cycle: Traverse the list with the slow and fast pointers. If a cycle exists, the fast pointer will eventually catch up to the slow pointer (i.e., they will point to the same node). If the fast pointer reaches the end of the list, then no cycle exists.

4. Return result: If the slow and fast pointers meet, then a cycle exists, so return true. Otherwise, return false.

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     public int val;
 *     public ListNode next;
 *     public ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public bool HasCycle(ListNode head) {

        if (head == null || head.next == null)
{
    return false;
}

var slow = head;
var fast = head.next;

while (slow != fast)
{
    if (fast == null || fast.next == null)
    {
        return false;
    }

    slow = slow.next;
    fast = fast.next.next;
}

return slow == fast;
    }
}

Complexity

Time Complexity: O(N)

Space Complexity: O(1)